圓周長計算:如何用英語流暢解釋這個數學概念? [Calculating Circumference: How to Explain This Mathematical Concept in Fluent English?]
![Circumference-圓周長計算:如何用英語流暢解釋這個數學概念? [Calculating Circumference: How to Explain This Mathematical Concept in Fluent English?]](https://littlenewton.efroip.tw/wp-content/uploads/2025/02/0.37637030364414437-300x200.png)
在數學的世界中, 圓周長的計算 是一個非常基本但同時也至關重要的概念。任何學習幾何的學生都會接觸到這個主題,而能夠流暢地用英語解釋這個數學概念,對於非母語學習者來說,更是一項挑戰。在這篇文章中,我們將探討圓周長的定義、公式和計算方法,並提供有效的教學資訊,幫助學習者克服語言障礙。
1. 圓和圓周長的定義
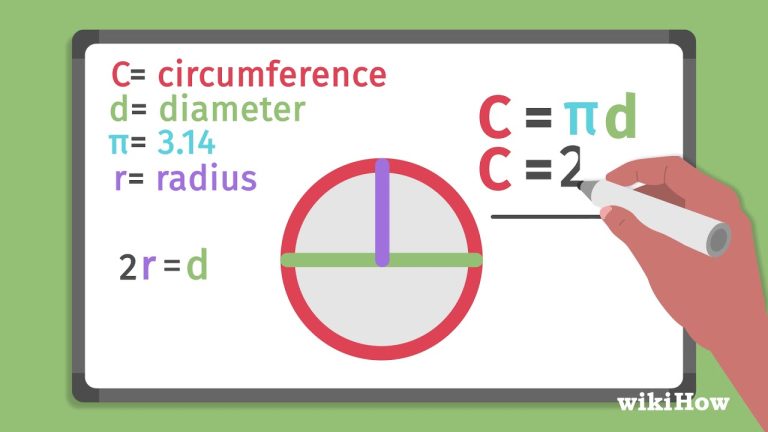
圓 是一種平面幾何圖形,定義為一個點(圓心)到所有邊界點的距離都相同的集合。這個距離稱為 半徑 (Radius),而圓周長則是圓的邊界長度。圓周長的計算涉及到圓的半徑或直徑(Diameter)。公式如下:
\[
\text{圓周長} = 2 \pi r \quad(其中 r 為半徑)
\]
\[
\text{圓周長} = \pi d \quad(其中 d 為直徑)
\]
這裡,數學常數 π (圓周率)大約為3.14,這是圓周長與其直徑之比的常數。
| 圓的元素 | 定義 |
|---|---|
| 半徑 (r) | 圓心到圓周的距離 |
| 直徑 (d) | 通過圓心的圓的最大直線長度,即 2r |
| 圓周長 | 圓的邊界的總長度 |
2. 圓周長的計算公式
為了計算圓周長,首先必須了解圓的半徑和直徑。對於許多學生而言, 記住公式 至關重要。在解釋這些公式時,應用實際例子來幫助學生理解。
例如,如果知道一個圓的半徑是5厘米,則圓周長計算如下:
\[
\text{圓周長} = 2 \pi \times 5 \approx 2 \times 3.14 \times 5 = 31.4 \text{厘米}
\]
同理,如果給定直徑為10厘米,則計算方式為:
\[
\text{圓周長} = \pi \times 10 \approx 3.14 \times 10 = 31.4 \text{厘米}
\]
這樣的例子不僅能幫助學生理解公式的應用,也能讓他們在使用英語解釋時更加自信。

3. 圓周長的實際應用
圓周長的計算在 許多日常生活中都非常有用 。比如,在建築設計、科學實驗和工業工程中,精確的計算圓周長對於測量和材料的選擇非常關鍵。理解圓周長的意義不僅體現在數學課堂上,也延伸到實際情境中。
例如,在設計一個圓形的游泳池時,工程師必須計算圓周長來確定周圍的圍欄長度和鋪設材料的數量。這裡的計算就會直接影響成本和安全。
| 實際應用案例 | 描述 |
|---|---|
| 游泳池設計 | 計算圓周長以確定圍欄的長度 |
| 零件製造 | 確保圓形零件的精確度 |
| 運動場規劃 | 計算圓形跑道的周長 |

4. 教學方法與策略
要想在教室裡有效地 教導圓周長的計算 ,教師可以採用多種教學策略。使用視覺輔助工具,例如圖表或模型,將幫助學生更易於理解。以下是一些有效的教學方法:
– 使用實體圓形物體(如圓形紙盤)讓學生親身測量半徑和直徑。
– 鼓勵學生在小組中討論他們的計算過程。
– 利用互動式軟體幫助學生觀看圓的幾何特徵。
這些方法能夠提高學生的參與感,同時增強他們對圓周長計算的理解和能力。

5. 克服語言障礙
對於非英語母語的學習者,圓周長計算的術語可能會造成理解上的困難。輔在學習數學術語的同時,學生應受到鼓勵將這些概念與日常語言聯繫起來。例如,學生可以用”圈”來理解半徑和直徑的概念,並形象化圓周長。
教師可以利用圖形化的網絡和詞彙表,幫助學生建構與數學相關的詞彙。在此過程中,教師應鼓勵學生自信地用英語表達他們的理解,無論是口頭還是書面。
| 語言支持策略 | 描述 |
|---|---|
| 圖詞卡 | 使用圖像幫助記憶數學術語 |
| 小組討論 | 鼓勵學生以英語表達思想 |
| 互動式教學工具 | 提供視覺和動手學習的機會 |
總結來看,圓周長的計算不僅是數學課程的一個重要話題,更是日常生活中應用廣泛的概念。 通過有效的教學方法與策略,以及克服語言障礙的努力,學生能夠更好地理解和計算圓周長,並用流暢的英語表達這一數學知識。
~ 旅行者的語言神器 ~

準備出國?Enjoy ABC 讓你輕鬆學會旅行必備語言!
✔ 實用短句:點餐、問路,馬上開口說。
✔ 文化小知識:融入當地,旅行更精彩。
✔ 離線學習:無網路也能隨時複習。


![推動AI向下扎根的3種方法|教育部新政解析:你不可忽視的未來英文競爭力關鍵 [3 Ways To Root AI Education Downwards | Ministry Of Education’s Policy Analysis: The Key To Future English Competitiveness]](https://littlenewton.efroip.tw/wp-content/uploads/2025/07/my_prefix_1752329549-768x512.png)

