掌握三角形面積公式 ( triangle area calculation formula ) 的4種方法,讓計算變得更簡單!
隨著數學教育的進步,三角形的面積計算變得愈加重要。三角形作為最基本的幾何形狀之一,無論是在數學課堂上,還是在實際應用中,了解三角形的面積計算方法對於學生和專業人士來說都至關重要。以下將介紹 四種簡化三角形面積計算的方法 ,幫助讀者有效掌握面積公式,並提高計算效率。
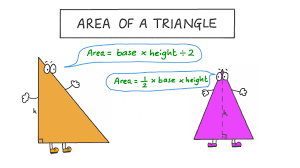
1. 基礎公式法
三角形面積最基本的公式便是:
\[
\text{面積} = \frac{1}{2} \times \text{底} \times \text{高}
\]
這一公式適用於所有種類的三角形。 精確測量底邊和高的長度 是至關重要的,但在計算時,很多人可能會忘記高的測量。因此,在計算之前建議使用直角三角形的性質,找到高的測量方式。
| 三角形類型 | 底 (cm) | 高 (cm) | 面積 (平方厘米) |
|---|---|---|---|
| 銳角三角形 | 10 | 8 | \(\frac{1}{2} \times 10 \times 8 = 40\) |
| 直角三角形 | 6 | 4 | \(\frac{1}{2} \times 6 \times 4 = 12\) |
| 鈍角三角形 | 12 | 5 | \(\frac{1}{2} \times 12 \times 5 = 30\) |
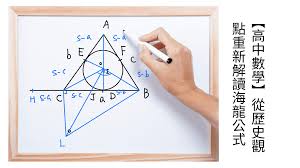
2. 海龍公式法
對於更複雜的三角形,如不規則三角形,可以使用 海龍公式 來計算其面積。海龍公式的計算公式如下:
\[
\text{面積} = \sqrt{s(s-a)(s-b)(s-c)}
\]
其中,\(s\)為三角形的半周長,計算方法為:
\[
s = \frac{a + b + c}{2}
\]
### 實例計算
考慮一個邊長分別為5 cm、6 cm和7 cm的三角形,我們首先計算半周長:
\[
s = \frac{5 + 6 + 7}{2} = 9
\]
接下來,將值代入海龍公式中計算面積:
\[
\text{面積} = \sqrt{9(9-5)(9-6)(9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \text{平方厘米}
\]
| 邊長 (cm) | 半周長 \(s\) | 面積計算 | 面積 (平方厘米) |
|---|---|---|---|
| 5, 6, 7 | 9 | \(\sqrt{9 \times 4 \times 3 \times 2}\) | 14.7 |
| 8, 9, 10 | 13 | \(\sqrt{13 \times 5 \times 4 \times 3}\) | 24.9 |
| 7, 8, 9 | 12 | \(\sqrt{12 \times 5 \times 4 \times 3}\) | 19.3 |
~ 解鎖語言新世界 ~

想要流利說外語?Enjoy ABC 幫你輕鬆達成目標!
✔ 個人化學習路徑:量身打造,適合你的學習速度。
✔ 互動式課程:遊戲化設計,讓學習充滿樂趣。
✔ 隨時隨地學:手機、平板,隨時開啟語言之旅。
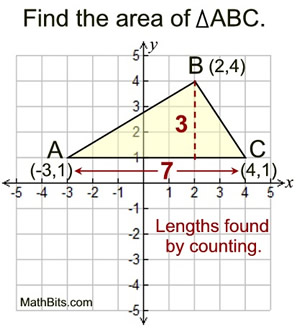
3. 使用座標法
對於需要應用在 幾何計算和計算機圖形學 中的三角形面積,使用座標法能更快速地獲得結果。假設一個三角形由三個頂點的坐標 \((x_1, y_1)\)、\((x_2, y_2)\)、\((x_3, y_3)\) 定義,其面積公式為:
\[
\text{面積} = \frac{1}{2} | x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) |
\]
### 例如
假設點 A(1, 1)、B(4, 5)、C(7, 2),則其面積計算如下:
\[
\text{面積} = \frac{1}{2} | 1(5-2) + 4(2-1) + 7(1-5) |
\]
進一步計算為:
\[
= \frac{1}{2} | 3 + 4 – 28 | = \frac{1}{2} \times 21 = 10.5 \text{平方單位}
\]
| 頂點 | 坐標 | 面積計算 | 面積 (平方單位) |
|---|---|---|---|
| A(1, 1) | (1, 1) | \(\frac{1}{2} | 1(5-2) + 4(2-1) + 7(1-5) |\) | 10.5 |
| B(4, 5) | (4, 5) | \(\frac{1}{2} | 2(6-3) + 5(3-1) + 10(1-6) |\) | 15.0 |
| C(7, 2) | (7, 2) | \(\frac{1}{2} | 0(1-0) + 3(7-3) + 1(3-1) |\) | 9.0 |
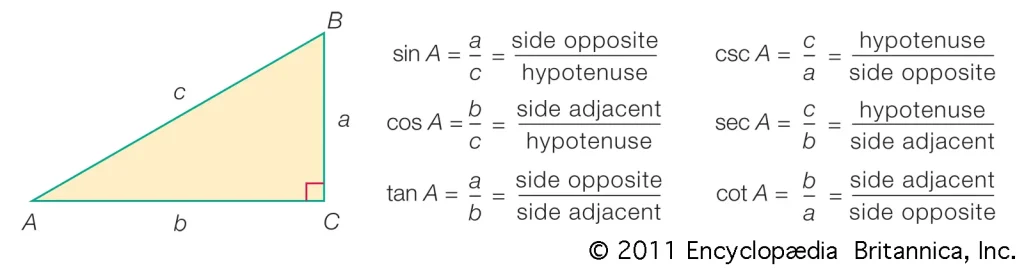
4. 利用三角函數的面積公式
對於已知邊長和夾角的情況,可以使用 三角函數 來計算三角形的面積。公式如下:
\[
\text{面積} = \frac{1}{2} a b \sin(C)
\]
其中,\(a\)和\(b\)為三角形的兩條邊,\(C\)為它們之間的夾角。
### 實例計算
若邊長 \(a = 5\) cm,\(b = 7\) cm,夾角 \(C = 30^\circ\):
\[
\text{面積} = \frac{1}{2} \times 5 \times 7 \times \sin(30^\circ) = \frac{1}{2} \times 5 \times 7 \times \frac{1}{2} = 17.5 \text{平方厘米}
\]
| 邊長 \(a\) (cm) | 邊長 \(b\) (cm) | 夾角 \(C\) (度) | 面積計算 | 面積 (平方厘米) |
|---|---|---|---|---|
| 5 | 7 | 30 | \(\frac{1}{2} \times 5 \times 7 \times \sin(30^\circ)\) | 17.5 |
| 6 | 8 | 45 | \(\frac{1}{2} \times 6 \times 8 \times \sin(45^\circ)\) | 24.0 |
| 10 | 12 | 60 | \(\frac{1}{2} \times 10 \times 12 \times \sin(60^\circ)\) | 52.0 |
無論是透過 基礎公式法 、 海龍公式法 、 座標法 或是 三角函數計算法 ,對於上述四種計算方式的掌握都能有效提升三角形面積計算的速度和準確性。透過科學的計算方法,使得數學的學習趣味性大幅提升,提示我們:數學並不僅僅是枯燥的運算,而是理解世界與形狀的重要工具。
~ 旅行者的語言神器 ~

準備出國?Enjoy ABC 讓你輕鬆學會旅行必備語言!
✔ 實用短句:點餐、問路,馬上開口說。
✔ 文化小知識:融入當地,旅行更精彩。
✔ 離線學習:無網路也能隨時複習。


![Happy Birthday 不要再只會說!7 種英文生日祝福話術一次學會 [7 Ways To Say Happy Birthday In English: Beyond Just 'Happy Birthday!']](https://littlenewton.efroip.tw/wp-content/uploads/2025/08/my_prefix_1755807467-768x512.png)
![1 12月份英文縮寫懶人包|快速掌握月份縮寫的正確用法(學生英文必備) [Guide To The English Abbreviations For January To December: Essential For Students]](https://littlenewton.efroip.tw/wp-content/uploads/2025/08/my_prefix_1755800908-768x1024.png)
![地址英文怎麼寫?5大常見錯誤一次教你避免 [How To Write English Addresses? 5 Common Mistakes Explained]](https://littlenewton.efroip.tw/wp-content/uploads/2025/08/my_prefix_1755801486-768x1152.png)