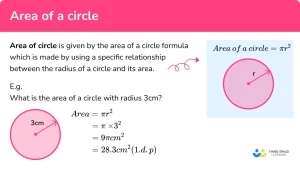
在數學學習中，圓的面積計算是學子們常必須面對的課題。雖然圓面積的公式 \(A = \pi r^2\) 看似簡單易懂，實際上卻有許多潛在的計算錯誤，可能讓學生在解題過程中遭遇障礙。以下是5個常見的陷阱，以及如何避免這些錯誤的建議。
1. 忘記圓的半徑轉換
在計算圓的面積時，學生經常會忽視半徑的單位轉換。舉例來說，如果半徑以公分（cm）提供，但需要以米（m）計算面積，則必須進行適當的轉換。這一點相當重要，因為不正確的單位會直接導致面積的計算錯誤。
| 陷阱編號 | 常見陷阱 | 解決方法 |
|---|---|---|
| 1 | 忘記圓的半徑轉換 | 確認使用正確的單位進行轉換 |
| 2 | 漏掉π符號 | 在最終答案中包含π，並標示具體數值 |
| 3 | 使用不正確的圓徑值 | 檢查計算前的圓徑或半徑數據 |
| 4 | 計算時誤將圓周與面積混淆 | 明確區分圓的面積與圓周的公式 |
| 5 | 忽略優先運算順序 | 按照數學運算優先級進行計算 |
2. 漏掉π符號
許多學生在計算圓面積時，容易忘記將π符號納入計算，或是在最終答案中不加區分地將數值表示為整數。正確的寫法應該是保留π，例如：若計算結果為20，可表示為 \(20\pi\) ，這樣更能準確表達其意義。
| 實際計算範例 | 半徑 (r) | 面積 (A = πr²) |
|---|---|---|
| 3 cm | 3 cm | \(9\pi\) cm² |
| 5 m | 5 m | \(25\pi\) m² |
3. 使用不正確的圓徑值
另一個常見的錯誤是使用錯誤的圓徑數值。學生在閱讀題目時可能將圓徑（d）與半徑（r）混淆，進而導致計算錯誤。圓徑是直徑的兩倍，因此在應用公式時，正確的代入值至關重要。
4. 計算時誤將圓周與面積混淆
另有一部分學生在計算圓的面積時，將圓周的公式誤用於面積計算。圓周長的計算公式為 \(C = 2\pi r\)，這與面積的計算徹底不同。因此，每位學生都應該確保自己理解這兩個公式的區別。
| 圓的公式 | 公式 |
|---|---|
| 圓的面積 | \(A = \pi r^2\) |
| 圓的周長 | \(C = 2\pi r\) |
5. 忽略優先運算順序
最後一個陷阱是忘記數學計算的運算優先級。例如，在計算圓的面積時，學生可能會先計算半徑的平方，再乘以π，這是正確的方式；但如忽略括號，或將計算順序顛倒，可能導致錯誤結果。
圓的面積計算是數學中相對容易掌握的部分，但細微的錯誤卻能造成非常實質的影響。通過避免以上提到的五個常見陷阱，每位學生都能提高計算準確度，建立良好的數學基礎。唯有在平時的學習中牢牢把握細節，才能更自信地面對未來的數學挑戰。
